The New Keynesian Model
Macroeconomics (M8674), May 2025
Vivaldo Mendes, ISCTE
vivaldo.mendes@iscte-iul.pt
1. Introduction
What is the New Keynesian Model (NKM)?
- It’s a DSGEM
- It’s a new version of the Old Keynesian model, which was:
- Following John Maynard Keynes from the 1930s
- Dominant until the late 1970’s
- Strictly based on Adaptive expectations
- Based on price and wage rigidities
- The NKM allows:
- Adapative and Rational Expectations
- Allows price and wage rigidities
Is the NKM Relevant today?
“Those criticisms notwithstanding, the New Keynesian model arguably remains the dominant framework in the classroom, in academic research, and in policy modeling.”
2. The Structure of the NKM
The Baseline New Keynesian Model
\[\begin{array}{lll} IS: & \hat{y}_{t} =\mathbb{E}_{t} \hat{y}_{t+1}-\frac{1}{\sigma}\left(i_{t}-\mathbb{E}_{t} \pi_{t+1}-r_{t}^{n}\right)+u_t \\ AS: & \pi_{t} = \kappa \hat{y}_{t}+\beta \mathbb{E}_{t} \pi_{t+1} +s_t \\ MP: & i_{t}=\pi_{t}+r_{t}^{n}+ \phi_{\pi}\left(\pi_{t}-\pi_{t}^{*}\right)+\phi_{y} \hat{y}_{t} \\ \text {Shocks : } & r_{t}^{n} =\rho_r \cdot r_{t-1}^{n}+\varepsilon^r_{t} \ , \quad u_{t} =\rho_u \cdot u_{t-1}+\varepsilon^u_{t} \ , \quad s_{t} =\rho_s \cdot s_{t-1}+\varepsilon^s_{t} \end{array}\]
- \(\{i,r_t^n,\hat{y},\pi, u_t, s_t,\varepsilon_t\}\): nominal interest rate, natural real interest rate, output-gap, inflation rate, demand shock, supply shock, and a random disturbance.
- \(\{\sigma,\kappa, \beta,\phi_{\pi},\phi_{y},\pi_{t}^{*},\rho\}\) are parameters
- Forward-looking variables: \(\hat{y}_{t}, \pi_{t}\)
- Backward-looking variables: \(r_{t}^{n},u_t,s_t\)
- Static variables: \(i_t\)
The IS curve
\[\color{blue} \hat{y}_{t}= \mathbb{E}_{t} \hat{y}_{t+1}-\frac{1}{\sigma}\left(i_{t}-\mathbb{E}_{t} \pi_{t+1}-r_{t}^{n}\right)+u_t\]
- \(\hat{y}_{t}\) represents the output-gap (% deviations of GDP from Potential GDP).
- \(\mathbb{E}_{t}\) is the conditional expectations operator.
- \(i_t\) is the short term nominal interest rate set by the central bank.
- \(\mathbb{E}_{t} \pi _{t+1}\) is the level of expected inflation for period \(t+1\).
- \(r_{t}^{n}\) is the natural level of the real interest rate.
- \(u_t\) is a demand shock.
- \(\sigma\) is a parameter (coefficient of relative risk aversion).
The AS curve
\[\color{blue} \pi_{t}=\kappa \hat{y}_{t} +\beta \mathbb{E}_{t} \pi_{t+1}+s_t\]
- \(\pi\) is the inflation rate
- \(\hat{y}_{t}\) is the output-gap
- \(s_t\) is a supply shock
- \(\kappa , \beta\) are parameters.
- \(\kappa\) gives the level of price rigidity in the economy:
- \(\kappa \rightarrow \infty\): total flexibility
- \(\kappa \rightarrow 0\): total rigidity
The Monetary Policy Rule
\[\color{blue} i_{t}=\pi_{t}+r_{t}^{n}+ \phi_{\pi}\left(\pi_{t}-\pi_{t}^{*}\right)+\phi_{y} \hat{y}_{t}\]
- This specific form of rule is called the “Taylor Rule”, following John Taylor (1993).
- \(i_t\) is the nominal interest rate set by the central bank.
- \(\pi_t\) is the inflation rate.
- \(r_{t}^{n}\) is the natural level of the real interest rate.
- \(\pi^*_t\) is the central bank’s target level for the inflation rate.
- \(\phi_{\pi}, \phi_x\) are parameters.
- When \(\pi_{t}-\pi_{t}^{*}=0\) and \(\hat{y}_{t}=0\), we have \(i_{t}=\pi_{t}+r_{t}^{n}\).
John Taylor (1993). Discretion versus policy rules in practice, Carnegie-Rochester conference series on public policy, 39, 195-214.
Policy Rules and How the Fed Uses Them
- In the website Policy Rules and How Policymakers Use Them, the Fed says they have 5 major rules they use in the decision making process:
- Taylor rule
- Balanced-approach rule
- ELB-adjusted rule
- Inertial rule
- First-difference rule
- The last two perform much better than the others (include a persistence term)
- The Taylor rule is used in this course because it: (i) explains the logic of using rules , an (ii) simplifies the algebra of the NKM
Target Inflation Rate
All central banks in advanced countries have an optimal value for inflation they want to achieve. This is called the inflation target \((\pi^*)\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~\)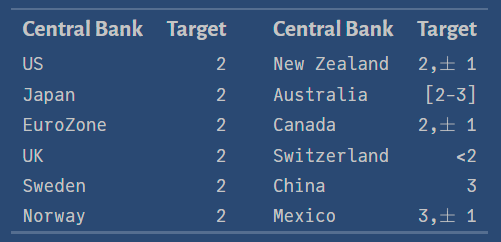
Source: Central Bank News
Why 2% Inflation?
According to the Swedish Central Bank (Sveriges Central Bank):
\(~~~~~~~~~\)
3. Some (illustrative) results
IRFs from a positive demand shock
\(~\)
u: demand shock s: supply shock y: output gap \(\pi\): inflation rate i: interest rate n: employment a: technology
IRFs from a negative supply shock
\(~\)
u: demand shock s: supply shock y: output gap \(\pi\): inflation rate i: interest rate n: employment a: technology
IRFs from the two shocks
\(~\)
u: demand shock s: supply shock y: output gap \(\pi\): inflation rate i: interest rate n: employment a: technology
Time-series from the two shocks
\(~\)
u: demand shock s: supply shock y: output gap \(\pi\): inflation rate i: interest rate n: employment a: technology
Heatmap: cross-correlation function (two shocks)
\(~\)
u: demand shock s: supply shock y: output gap \(\pi\): inflation rate i: interest rate n: employment a: technology
Standard deviation (two shocks)
\(~~~~~~~~~~~~~~~~~\)
4. Some criticisms of the NKM
Dominant model … but with alleged problems
Three main criticisms have been raised against the NKM: - Counter-intuitive results in the AS curve. - Counter-intuitive results in the IS curve. - Lack of persistence
Some influential criticisms
The IS and AS curves (allegedly) lead to easily refutable results. See, e.g.: - Ball, L. (1994). “Credible disinflation with staggered price-setting.”American Economic Review, 84(1), 282–289. - Fuhrer, J. and Moore, G. (1995). “Inflation persistence.” Quarterly Journal of Economics, 110(1), 127–159, February. - Fuhrer, J. (1995). The Persistence of Inflation and the Cost of Disinflation, New England Economic Review, January/February 1995, 3-16. - Canzoneri, M. B., Cumby, R. E., and Diba, B. T. (2007). Euler equations and money market interest rates: A challenge for monetary policy models, Journal of Monetary Economics, 54(7), 1863-1881.
Counter-intuitive results in the AS curve
- Consider the AS curve and ignore any shocks \((s_t=0)\):
\(\color{blue} \qquad \pi_{t}=\kappa \hat{y}_{t} +\beta \mathbb{E}_{t} \pi_{t+1}+s_t \quad \Rightarrow \quad\pi_{t}- \beta \mathbb{E}_{t} \pi_{t+1}=\kappa \hat{y}_{t} +s_t\)
“If the Federal Reserve engineers a disinflation, it does so by pursuing a contractionary monetary policy that lowers output below potential \((\hat{y}_{t}<0)\). But the flexible inflation model of the equation [above] says that when output falls short of potential, expected inflation in the next period must exceed current inflation. This does not sound like a disinflation”. Fuhrer (1995), page 9 - For simplicity assume \(s_t=0\),\(\ \kappa =1\), \(\beta=1\). A central bank could reduce inflation and produce higher expected inflation at the same time (see next slide for details):
\[ \underbrace{\pi_t-\mathbb{E}_t \pi_{t+1}}_{-2 \%}=\underbrace{\hat{y}_t}_{-2 \%} \]
Furher’s argument in more detail
Suppose the economy is in a stable situation: \(\pi_t = 2\% \ , \ \mathbb{E}_{t} {\pi}_{t+1}=2\% \ , \ \hat{y}_{t}=0\%\) \[\underbrace{\pi_t}_{2\%} - \underbrace{\mathbb{E}_{t} {\pi}_{t+1} }_{2\%} = \underbrace{\hat{y}_{t}}_{0\%} \]
Now, suppose inflation increases to \(3\%\). Normally, higher inflation forces the central bank to increase nominal interest rates, in order to reduce aggregate demand, which in turn will lead to a decrease in inflation and expected inflation.
However, this is not what happens in the AS curve. If inflation goes up to \(3\%\), and the central bank creates a recession of \(\hat{y}_{t}={-1\%}\) , we have to get: \[\underbrace{\pi_t}_{3\%} - \underbrace{\mathbb{E}_{t} {\pi}_{t+1} }_{4\%} = \underbrace{\hat{y}_{t}}_{-1\%} \]
It does not make sense: inflation goes up, the central bank creates a recession, and expected inflation goes up. In reality, \(\mathbb{E}_{t} {\pi}_{t+1}\) should go down, not up!
Counter-intuitive results in the IS curve
Consider the IS curve. Put the term \(\mathbb{E}_{t} \hat{y}_{t+1}\) on its left hand side:
\[\color{blue} \hat{y}_{t} - \mathbb{E}_{t} \hat{y}_{t+1} = -\frac{1}{\sigma}\left(i_{t}-\mathbb{E}_{t} \pi_{t+1}-r_{t}^{n}\right)+u_t\]
“An awkward implication of [this equation] is that, when the real interest rate rises above its steady-state level, the level of consumption must decrease, but its change must be expected to increase.” Estrella and Furher (2002), page 1021
For simplicity assume \((u_t=0)\) and \(\sigma=1\): The IS seems to give a strange result: \[[(i_{t}-\mathbb{E}_{t} \pi_{t+1}) >r_{t}^{n}] \Rightarrow (\hat{y}_{t} < \mathbb{E}_{t} \hat{y}_{t+1})\]
The central bank may increase \(i_t\) to fight inflation, and the expected output-gap is supposed to increase. Does not make sense (more details in next slide).
Furher&Estrella’s argument in more detail
- Suppose the economy is initially in a stable situation: \(i_t = 3\%, \ , \ \mathbb{E}_{t} {\pi}_{t+1}=2\% \ , r^n_t = 1\% ,\ \hat{y}_{t}=0\%, \mathbb{E}_t \hat{y}_{t+1}=0\%\) \[\underbrace{i_t}_{3\%} - \underbrace{\mathbb{E}_{t} {\pi}_{t+1} }_{2\%} - \underbrace{r^n_t}_{1\%}= -(\underbrace{\hat{y}_{t}}_{0\%} - \underbrace{\mathbb{E}_{t} \hat{y}_{t+1}}_{0\%})\]
- Now, suppose the central bank increases nominal interest rates to \(4\%\). This should lead to the expected output gap to go down, because an increase in \(i_t\) must constrain aggregate demand and economic activity.
- However, that is not what happens in the IS curve:
\[\underbrace{i_t}_{4\%} - \underbrace{\mathbb{E}_{t} {\pi}_{t+1} }_{2\%} - \underbrace{r^n_t}_{1\%}= -(\underbrace{\hat{y}_{t}}_{0\%} - \underbrace{\mathbb{E}_{t} \hat{y}_{t+1}}_{1\%})\]
- An increase in \(i_t\) leads to an increase in the expected output gap: it doses not make sense.
The shapes of the IRFs are wrong
- In macroeconomics, most variables respond to a shock gradually.
\(~\)
Their IRFs are hump-shaped, like the one on the left, very different from the NKM ones.
5. Refuting the criticisms
Does an increase in \(i\) lead to a boom?
- What happens if the central bank decides (for whatever reason) a sharp increase in its nominal interest rate?
- It causes a recession and a slight reduction in inflation: \({\ \color{blue}{\uparrow i_t \ \Rightarrow \ \downarrow \pi, \downarrow \hat{y}}}\)
- It does not cause an increase in the expected output gap as the criticism of the IS curve above suggested.
- This is a vindication of the NKM and exposes the limitations of that criticism.
- See the following figure.
\(~\)
u: demand shock s: supply shock e: interest-rate shock y: output gap \(\pi\): inflation rate i: interest rate n: employment a: technology
Does the fight of inflation lead to higher inflation?
- Suppose there is a negative supply shock that leads to higher inflation.
- The criticism above regarding the AS curve suggests that disinflationary measures should lead to higher inflation expectations.
- Is this correct?
- The central bank sharply raises nominal interest rates to fight inflation.
- The IFRs can be found below. Anything wrong with them?
- No! In fact, \({\ \color{blue}{\uparrow i_t \ \Rightarrow \ \downarrow \pi, \downarrow \hat{y}}}\)
\(~\)
u: demand shock s: supply shock e: interest-rate shock y: output gap \(\pi\): inflation rate i: interest rate n: employment a: technology
The NKM with inflation and output persistence
- To overcome the problem of hump-shaped IRFs we need to do two things:
- Introduce lagged inflation in the AS curve
- Introduce lagged output in the IS curve
- So the problem is not with the model, but whether we omit (or not) fundamental parts of reality.
\[\begin{array}{lll} IS: & \hat{y}_{t} = {\color{blue}{\varphi \hat{y}_{t-1}}} + {\color{blue}{(1-\varphi)}}\mathbb{E}_{t} \hat{y}_{t+1}-\frac{1}{\sigma}\left(i_{t}-\mathbb{E}_{t} \pi_{t+1}-r_{t}^{n}\right)+u_t \\ AS: & \pi_{t} ={\color{blue}{\mu \pi_{t-1}}}+\kappa \hat{y}_{t}+\beta \mathbb{E}_{t}\pi_{t+1} +s_t \ , \qquad \ {\color{blue}{\beta =1-\mu}}\\ MP: & i_{t}=\pi_{t}+r_{t}^{n}+ \phi_{\pi}\left(\pi_{t}-\pi_{t}^{*}\right)+\phi_{y} \hat{y}_{t} \\ \text {Shocks : } & r_{t}^{n} =\rho_r \cdot r_{t-1}^{n}+\varepsilon^r_{t} \ , \quad u_{t} =\rho_u \cdot u_{t-1}+\varepsilon^u_{t} \ , \quad s_{t} =\rho_s \cdot s_{t-1}+\varepsilon^s_{t} \end{array}\]
Hump-shaped IRFs in the NKM
\(~\)
\(\varphi = 0.6 \ , \mu = 0.9\)
Appendix A
Derivation of the AD Curve (not required in the evaluation process)
Maximization of Utility
- Households maximize utility \((u)\) which depends on consumption \((c)\) over time
\[u(c_t)+ \mathbb{E}_{t}u(c_{t+1})+...\]
Subject to a constraint in every period
\[t: \qquad \ \quad \ \ \ \cal{B}_{t} + \cal{P}_{t} c_t = \cal{P}_{t} w_t \qquad \qquad \qquad \] \[t+1: \qquad \underbrace{{\cal{B}}_{t+1}}_{=0} + {\cal{P}}_{t+1} c_{t+1} = {\cal{P}}_{t+1} w_{t+1} + {\cal{B}}_{t}(1+i_t)\]
\(c\) is real consumption, \(\cal{P}\) is the price level, \(w\) is the real wage, \(i\) is the nominal interest rate, and \(\cal{B}\) is the level of nominal bonds
\({\cal{B}}_{t+1}=0\): it does not make sense to have positive savings in some last period
The Lagrangian Function and FOCs
The maximization of utility is given by the Lagrangian function \((\cal{L})\) \[\max_{c_{t}, c_{t+1}, \cal{B}_{t}} \cal{L}=\beta^{t}\left[u\left(c_{t}\right)+\lambda_{t}\left(w_{t}-P_{t} c_{t}-B_{t}\right)\right] + \qquad \qquad \qquad \qquad \]
\[\qquad \quad \quad \beta^{t+1}\left[u\left(c_{t+1}\right)+\lambda_{t+1}\left(w_{t+1}- {\cal{P}}_{t+1} c_{t+1}+ (1+i_t)B_{t}\right)\right]\]
and the First Order Conditions (FOCs) are: $$ \[\begin{aligned} &\frac{\partial \cal{L}}{\partial c_{t}}=0 \Rightarrow \beta^{t}\left [u^{\prime}\left(c_{t}\right)-\lambda_{t} \cal{P}_{t}\right]=0 \Rightarrow {\color{blue} u^{\prime}\left(c_{t}\right)/\cal{P}_{t}=\lambda_{t}} \\ &\frac{\partial \cal{L}}{\partial c_{t+1}}=0 \Rightarrow \beta^{t+1}\left[u^{\prime}\left(c_{t+1}\right)-\lambda_{t+1} {\cal{P}}_{t+1}\right]=0 \Rightarrow {\color{blue} u^{\prime} \left(c_{t+1}\right)/{\cal{P}}_{t+1}=\lambda_{t+1}} \\ &\frac{\partial \cal{L}}{\partial \cal{B}_{t}}=0 \Rightarrow-\beta^{t} \lambda_{t}+\beta^{t+1} \lambda_{t+1}\left(1+i_{t}\right)=0 \Rightarrow {\color{blue} \lambda_{t}=\beta \lambda_{t+1}\left(1+i_{t}\right)} \end{aligned}\]$$
The Euler equation
From the three FOCs
\[{\color{blue} u^{\prime}\left(c_{t}\right)/\cal{P}_{t}=\lambda_{t}} \quad , \quad {\color{blue} u^{\prime}\left(c_{t+1}\right)/ {\cal{P}}_{t+1}=\lambda_{t+1}} \quad , \quad {\color{blue} \lambda_{t}=\beta \lambda_{t+1}\left(1+i_{t}\right)} \]
we can obtain:
\[\frac{u^{\prime}\left(c_{t}\right)}{\cal{P}_{t}}=\beta \frac{u^{\prime}\left(c_{t+1}\right)}{{\cal{P}}_{t+1}}(1+i_t)\]
simplifying
\[ u^{\prime}\left(c_{t}\right)=\beta \cdot u^{\prime}\left(c_{t+1}\right)(1+i_t)\frac{\cal{P}_{t}}{{\cal{P}}_{t+1}}\]
Now, \(\frac{\cal{P}_{t}}{{\cal{P}}_{t+1}} = \frac{1}{1+\pi_{t+1}}\), where \(\pi_{t+1}\) is the inflation rate at \(t+1\), so:
\[ u^{\prime}\left(c_{t}\right)=\beta \cdot u^{\prime}\left(c_{t+1}\right)\frac{1+i_t}{1+\pi_{t+1}}\]
Uncertainty and the Euler Equation
\[ u^{\prime}\left(c_{t}\right)=\beta \cdot u^{\prime}\left(c_{t+1}\right)\frac{1+i_t}{1+\pi_{t+1}}\]
- The Euler equation gives the optimal trade-off between consumption today versus consumption in the future
- But the future is not known with certainty, so the variables expressed with \(t+1\) will have to be taken under the expectations operator
\[ u^{\prime}\left(c_{t}\right)=\beta \cdot \mathbb{E}_{t} \left\{ u^{\prime}\left(c_{t+1}\right) \frac{1+i_{t}}{1+\pi_{t+1}} \right\}\]
Marginal utility of current consumption divided by its cost \((u'(c_t)/(1+i_t))\) is equal to the discounted value of the expected marginal utility of future consumption, divided by its expected cost \((\mathbb{E}_{t} \left\{u'(c_{t+1})/(1+\pi_{t+1}) \right\})\).
A CRRA Utility Function
\(~~~~~~~~~~~~\)
A CRRA Utility Function and the Euler equation
- A typical utility function is a CRRA
\[u (c_t) = \frac{c_{t}^{1-\sigma} - 1}{1-\sigma} \quad \Rightarrow \quad u'(c_t) = c_{t}^{-\sigma}\]
- where \(\sigma \geq 0\) is the coefficient of relative risk aversion: \[ -\frac{c \cdot u^{\prime \prime}(c)}{u^{\prime}(c)}=\frac{-c\left(-\sigma c^{-\sigma-1}\right)}{c^{-\sigma}}=\sigma \]
- Inserting this marginal utility \((u'(c_t))\) into the Euler equation gives:
\[ c_{t}^{-\sigma}=\beta \cdot \mathbb{E}_{t}\left\{c_{t+1}^{-\sigma} \left[ \frac{1+i_{t}}{1+\pi_{t+1}} \right] \right\}\]
Applying logs to the Euler equation
- Applying logs to the Euler equation
\[-\sigma \ln c_{t}= \ln \beta + \mathbb{E}_{t}\left\{ -\sigma \ln c_{t+1} + {\color{blue} \ln\left[ \frac{1+i_{t}}{1+\pi_{t+1}} \right] } \right\}\]
- If \((i,\pi)\) are small values, then
\[\ln(1+i)\approx i \quad , \quad \ln(1+\pi)\approx \pi\]
- So, the log version of the Euler equation will look like:
\[ -\sigma \ln c_{t}= \ln \beta + \mathbb{E}_{t} (-\sigma \ln c_{t+1} + \underbrace{i_t - \pi_{t+1}}_{r_{t}}) \tag{1}\]
- The Euler eq. in the steady-state (notice that \(r^n_t\) is the natural real interest rate):
\[ -\sigma \ln \overline{c}_{t}= \ln \beta + \mathbb{E}_{t} (-\sigma \ln \overline{c}_{t+1} + r^n_t) \tag{2} \]
Percentage Deviations from the Steady-state
Subtract eq. (2) from (1), and get consumption as a % deviation from steady-state: \[\hat{c}_t = \ln c_t - \ln \overline{c}_{t}\]
Therefore:
\[-\sigma \ln c_{t}-\sigma \ln \overline{c}_{t}= \cancel{\ln \beta} + \mathbb{E}_{t} (-\sigma \ln c_{t+1} + i_t - \pi_{t+1}) - \cancel{\ln \beta} + \mathbb{E}_{t} (-\sigma \ln \overline{c}_{t+1} + r^n_t) \]
\[-\sigma \hat{c}_{t} = \mathbb{E}_{t} (-\sigma \hat{c}_{t+1} + i_{t} - \pi_{t+1} -r^n_t)\]
- That is:
\[ \hat{c}_{t} = \mathbb{E}_{t} \hat{c}_{t+1} - \frac{1}{\sigma} \left( i_{t} - \mathbb{E}_{t} \pi_{t+1} -r^n_t \right) \tag{3}\]
Aggregate demand
- To make things as easy as possible, consider an economy where aggregate demand (or GDP) is determined by
\[ y_t = c_t + g_t \tag{4}\]
\(y_t\) is real GDP, \(c_t\) is real consumption, \(g_t\) stands for real government spending.
This means that there are no Investment expenditures, nor Exports or Imports.
Applying growth rates to the eq. (4), we get
\[{\color{blue} \hat {y}_t = \gamma \hat {c}_t + (1-\gamma)\hat {g}_t} \tag{5}\]
- where \(\gamma = \overline{c}/ \overline{y}\) and \((1-\gamma) = \overline{g}/\overline{y}\), and \(\overline {c}, \overline {y}, \overline {g}\) are the steady-state values.
The IS function (I)
- The simplest economy is one where GDP \((y_t)\) is equal to consumption.
- This is the case when \(\gamma=1\) in eq. (5):
\[y_t = c_t \quad \Rightarrow \quad \hat {y}_t = \hat{c}_t\]
- Therefore
\[{\color{blue} \hat{y}_{t} = \mathbb{E}_{t} \hat{y}_{t+1} - \frac{1}{\sigma}( i_{t} - \mathbb{E}_{t} \pi_{t+1} -r^n_t)} \tag{6}\]
- The output-gap \((\hat {y}_t)\) depends upon the expected output gap \((\mathbb{E}_{t} \hat{y}_{t+1})\), and the difference between the expected real interest rate \((i_{t} - \mathbb{E}_{t} \pi_{t+1})\) and the natural real interest rate \((r^n_t)\).
The IS function with Government Spending (I)
- Now, consider that \(\gamma<1\), implying the existence of public spending.
- To derivate the IS function, insert eq. (3) into (5) which leads to
\[ \hat{y}_{t}=\gamma\left[\mathbb{E}_{t} \hat{c}_{t+1}-\frac{1}{\sigma}\left(i_{t}- \mathbb{E}_{t} \pi_{t+1}-r_{t}^{n}\right)\right]+(1-\gamma) \hat{g}_{t} \tag{7} \]
- Then, from eq. (5) we can obtain
\[ \gamma \mathbb{E}_{t} \hat{c}_{t+1}=\mathbb{E}_{t} \hat{y}_{t+1}-(1-\gamma) \mathbb{E}_{t} \hat{g}_{t+1} \tag{8} \]
- Now, insert eq. (8) into (7), and simplify to obtain the IS function:
\[ {\color{blue} \hat{y}_{t}=\mathbb{E}_{t} \hat{y}_{t+1}-\frac{\gamma}{\sigma}\left(i_{t}- \mathbb{E}_{t} \pi_{t+1}-r_{t}^{n}\right)+(1-\gamma)\left(\hat{g}_{t}- \mathbb{E}_{t} \hat{g}_{t+1}\right)} \tag{9} \]
The IS function with Government Spending (II)
- Another way of expressing the demand side of the economy is to have two equations (instead of just one, as in eq. 9). These two are:
- The linearized Euler equation:
\[{\color{blue} \hat{c}_{t} = \mathbb{E}_{t} \hat{c}_{t+1} - \frac{1}{\sigma} \left( i_{t} - \mathbb{E}_{t} \pi_{t+1} -r^n_t \right)} \tag{3'}\] - The linearized aggregate demand equation
\[{\color{blue} \hat {y}_t = \gamma \hat {c}_t + (1-\gamma)\hat {g}_t} \tag{5'} \]
- These two equations display the inter-relationships between consumption, output, and government spending, the expected real interest rate, and the natural real interest rate.
Current vs future consumption: graphical analysis
| \(C_t\) vs \(C_{t+1}\): prices | \(C_t\) vs \(C_{t+1}\): preferences |
|---|---|
The optimal consumption pattern: graphical analysis
\(~~~~~~~~~~~~~~~~\)
Appendix B
Derivation of the AS Curve (not required in the evaluation process)
Price Rigity: three different ways … similar results
John M. Roberts (1995). “New Keynesian economics and the Phillips curve,” Journal of Money, Credit, and Banking, 27(4), 975–984.
Shows that the 3 papers below lead to similar results:
- John Taylor (1979). “Staggered Wage Setting in a Macro Model,” American Economic Review, P&P, Vol. 69, 108-113.
- Julio Rotemberg (1982), “Monopolistic price adjustment and aggregate output,” Review of Economic Studies, 49(4), 517–531.
- Guillermo Calvo (1983). “Staggered prices in a utility-maximizing framework”, Journal of Monetary Economics, 12(3), 383-398.
We will follow Calvo’s pricing.
Main assumptions: Calvo Pricing
- A1. In each period, a proportion of firms \((\theta)\) do not reset their prices.
- A2. There is monopolistic competition in the goods market: firms set prices (the optimal price, \(p^*_t)\) with a markup \((\ell)\) over marginal costs \((mc_{t})\). In logs:
\[ p_{t}^{*}=\ell+m c_{t} \tag{10}\]
- A3. Firms know that the price they set today \((z_t)\) remains constant during some time. So \(z_t\) is set to minimize the profit loss for not resetting prices.
- A4. Real marginal cost in logs \((mc_t - p_t)\) depends on the output gap \((\hat{y}_t)\)
\[m c_{t}-p_{t}=\psi \hat{y}_t\]
Monopolistic competition pricing
From: Hal Varian (2010). Intermediate Microeconomics: A Modern Approach, 8th Ed.
\(~~~~~~~~~~~~~~~~\)
Minimizing the Loss function
- Given assumptions A1 and A3, the Loss function \(L(z_t)\) is given by
\[ L\left(z_{t}\right)=\sum_{n=0}^{\infty}(\theta \beta)^{n} \cdot \underbrace{\mathbb{E}_{t}\left(z_{t}-p_{t+n}^{*}\right)^{2}}_{\text {expected profit loss}} \tag{11}\]
- \(z_t\) is the (log) price level that minimizes the losses until \(t+n\)
- \(\beta\) is a time discount factor
- \(\theta^n\) is the probability of having the price constant until \(t + n\)
- To minimize \(L(z_t)\)
\[\frac{\partial L}{\partial z_{t}}=0 \Rightarrow 2 \sum_{n=0}^{\infty}(\theta \beta)^{n} \cdot \mathbb{E}_{t}\left(z_{t}-p_{t+n}^{*}\right)=0\]
Minimizing the Loss function (cont.)
\[2 \sum_{n=0}^{\infty}(\theta \beta)^{n} \cdot \mathbb{E}_{t}\left(z_{t}-p_{t+n}^{*}\right)=0\]
\[\underbrace{\sum_{n=0}^{\infty}(\theta \beta)^{n} \cdot z_{t}}_{=\frac{1}{1-\theta \beta} \cdot z_{t}}=\sum_{n=0}^{\infty}(\theta \beta)^{n} \cdot \mathbb{E} p_{t+n}^{*}\]
\[ z_{t}=(1-\theta \beta) \sum_{n=0}^{\infty}(\theta \beta)^{n} \cdot \mathbb{E}_{t} p_{t+n}^{*} \tag{12}\]
The price set by firms \((z_t)\) is an exponential smoothing process of the prices set in the future if there were no price rigidities.
Markup and Marginal Costs
- In eq. (12), \(z_t\) depends on the optimal price level \((p_{t+n}^{*})\).
- But according to A2, the latter depends on the markup \((\ell)\) and on the marginal cost \((mc_t)\)
\[ p_{t}^{*}=\ell+m c_{t}\]
- Inserting this equation into eq. (12), leads to:
\[ z_{t}=(1-\theta \beta) \sum_{n=0}^{\infty}(\theta \beta)^{n} \cdot \mathbb{E}_{t}\left(\ell+m c_{t+n}\right) \tag{13}\]
- Firms set prices today depending on the expected levels of markups they are able to impose and on the expected levels of marginal costs.
The Aggregate Price level
- In the entire economy, the aggregate price level \((p_t)\) is easy to obtain following assumptions A1 and A3.
- \(\theta\) is the proportion of firms that keep prices unchanged.
- \(1-\theta\) is the proportion of firms that reset current prices.
- Therefore, the aggregate price level in logs \((p_t)\) has to be given by:
\[p_{t}=\theta \cdot p_{t-1}+(1-\theta) \cdot z_{t}\]
- Solving for \(z_t\), leads to:
\[\qquad \qquad \qquad \qquad \qquad z_{t}=\frac{1}{1-\theta}\left(p_{t}-\theta p_{t-1}\right) \tag{14}\]
- \(p_{t-1}\) is the last period’s aggregate price level, \(z_t\) is the new reset price.
A crucial trick
- To write eq. (13) in a more useful manner, we have to apply a trick.
- From the solution to RE models, one may recall that, if we have an equation:
\[y_{t}=a \cdot x_{t}+b \cdot\mathbb{E}_{t} y_{t+1}\]
- … we will get a solution as follows (provided that \(|b|<1\)):
\[y_{t}=a \sum_{n=0}^{\infty} b^{n} \cdot \mathbb{E}_{t} x_{t+n}\]
- Therefore, as \((|\theta \beta|<1)\), eq. (13) has to be the solution to the equation:
\[ z_{t}=\theta \beta \cdot \mathbb{E}_{t} z_{t+1}+(1-\theta \beta)\left(\ell+m c_{t}\right) \tag{15}\]
- Now, we can solve our problem, using equations (15) and (14.)
Solving the model
- From eq. (14) we get:
\[z_{t}=\frac{1}{1-\theta}\left(p_{t}-\theta p_{t-1}\right)\]
- And from eq. (15) we have:
\[z_{t}=\theta \beta \cdot E_{t} z_{t+1}+(1-\theta \beta)\left(\ell+m c_{t}\right)\]
- Equalizing both equations leads to
\[\frac{1}{1-\theta}\left(p_{t}-\theta p_{t-1}\right)=\theta \beta \cdot \frac{1}{1-\theta}\left(E_{t} p_{t+1}-\theta p_{t}\right)+(1-\theta \beta)\left(\ell+m c_{t}\right)\]
- Now, we have to simplify this equality:
- Multiply both sides by \(1-\theta\) and subtract \(p_t\) from both sides.
Simplifying
- After multiplying both sides by \(1-\theta\), we will get
\[p_{t}\left(1+\theta^{2} \beta\right)-\theta p_{t-1}=\theta \beta \mathbb{E}_{t} p_{t+1}+(1-\theta)(1-\theta \beta) (\ell + m c_{t})\]
- After subtracting \(p_t\) from both sides, and defining \(\mathbb{E}_{t} \pi_{t+1} = \mathbb{E}_{t} p_{t+1} -p_t\)
\[\underbrace{\left(\frac{1+\theta^{2} \beta -\beta \theta}{\theta}\right)}_{1+\frac{(1-\theta)(1-\theta \beta)}{\theta}} \cdot \ p_{t}-p_{t-1}=\beta \mathbb{E}_{t} \pi_{t+1}+\frac{(1-\theta)(1-\theta \beta)}{\theta} (\ell + m c_{t})\]
- We finally get:
\[\underbrace{\pi_{t}}_{p_{t}-p_{t-1}}=\beta \mathbb{E}_{t} \pi_{t+1}+\frac{(1-\theta)(1-\theta \beta)}{\theta}(\ell+\underbrace{\left.m c_{t}-p_{t}\right)}_{\text {real marg.cost }} \tag{16}\]
Final step: the NK Phillips Curve
- Now bring back assumption A4:
\[m c_{t}-p_{t}=\psi \hat{y}_t\]
- Inserting this into eq. (16)
\[\pi_{t}=\beta \mathbb{E}_{t} \pi_{t+1}+\frac{(1-\theta)(1-\theta \beta)}{\theta}(\ell+\psi \hat{y}_t)\]
- If one wants to abstract from markup costs, then \((\ell = 0)\), and the conventional New Keynesian Phillips Curve (also known as the AS function), is given by:
\[\qquad \qquad \qquad \qquad \qquad {\color{blue}\pi_{t}=\beta \cdot \mathbb{E}_{t} \pi_{t+1}+\kappa \cdot \hat{y}_t}\qquad \qquad \qquad \qquad \qquad (17)\]
- with: \(\kappa=\frac{\psi(1-\theta)(1-\theta \beta)}{\theta}.\)
- In the NKPC, inflation depends on expected inflation and the output gap.
Readings
- For the derivation of the IS function, read:
- Ulf Soderstrom (2006). “A simple model for monetary policy analysis”, Lecture notes, IGIER, Università Bocconi. (read pages 1-4)
- For the derivation of the AS function, read:
- Karl E. Whelan (2008). “The New-Keynesian Phillips Curve”, Lecture notes, University College Dublin. (read pages 4-8)