marp: true author: Vivaldo Mendes paginate: true style: | .columns { display: grid; grid-template-columns: minmax(0, 50fr) minmax(0, 50fr); } h2 { position: absolute; top: 50px; left: 75px; right: 75px; color: #34429a; font-size: 46px; }
h1 { font-size: 60px }
Filters & Impulse Response Functions
Macroeconomics (M8674), March 2025
Vivaldo Mendes, ISCTE
vivaldo.mendes@iscte-iul.pt
1. Filters
Types of Filters
- Main objective: to separate the long-run trend from the short-run cyclical component of a time series \(y(t)\) .
- There are various approaches to achieve this:
- Linear filter
- Linear filter with breaks
- Nonlinear filters
- Nonlinear filters
- Hodrick-Prescott filter (Hodrick & Prescott, 1997)
- Band Pass filter (Baxter & King, 1999)
- Hamilton filter (James Hamilton, 2017)
- … and some others
The Hodrick-Prescott filter (HP)
The HP filter is the most used filter in macroeconomics
It is given by the minimization problem:
\[\min _{\tau_{t}} \sum_{t=1}^{T}\left\{\left(y_{t}-\tau_{t}\right)^{2}+\lambda\left[\left(\tau_{t+1}-\tau_{t}\right)-\left(\tau_{t}-\tau_{t-1}\right)\right]^{2}\right\} \tag{1}\]
where:
- \(y_t\) is the observed time series
- \(\tau_t\) is the smooth trend that we want to obtain
- \(\lambda\) is the parameter that we set to obtain the desired smoothness in the trend
The HP filter: Special Cases
The value given to parameter \(\lambda\) is a choice of ours:
\[\min _{\tau_{t}} \sum_{t=1}^{T}\left\{\left(y_{t}-\tau_{t}\right)^{2}+\ {\color{blue}\lambda} \left[\left(\tau_{t+1}-\tau_{t}\right)-\left(\tau_{t}-\tau_{t-1}\right)\right]^{2}\right\}\]
- \(\lambda = 0\) \(\Rightarrow\) trivial solution because there are no cycles : \(y_t= \tau_t, \forall t\)
- \(\lambda \rightarrow \infty \Rightarrow\) linear trend leads to huge cycles between \(y_t\) and \(\tau_t\)
- \(\lambda = 1600\) \(\Rightarrow\) duration/amplitude of cycles acceptable for quarterly data
- \(\lambda = 7\) \(\Rightarrow\) duration/amplitude of cycles acceptable for annual data
- There is no “unquestionable” value for \(\lambda\)
The HP Filter: an Example
- Main objective: obtain cycles as % deviations from the trend
- This has an important implication:
- Time series with a trend: apply logs to the data before extracting the trend and the cycles
- Time series without a clear trend: do not apply logs to the data
- Quarterly data: “US_data.csv”
- A simple example:
- Real GDP (GDP)
- Consumer Price Index (CPI)
- Unemployment Rate (UR)
Dealing with rows and columns in a Matrix
\(~~~~~~~~~~~~\)
Compute the HP filter: a single variable
\(~~~~~~\)
Compute the HP filter: a single variable (another way)
\(~~~~~~\)
Compute the HP filter: several variables
\(~~~~~~\)
Compute the business-cycles: several variables
\(~~~~~~\)
Business cycles: Inflation and Unemployment
\(~~~~~~~~~~~~~~~~\)The inflation-gap \(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\)The unemployment-gap
The output-gap: logs vs levels
\(~~~~~~\) Correctly measured: using logs \(~~~~~~~~~~~~~~~~~~~\)Incorrectly measured: using levels
2. Impulse Response Functions
What are IRFs?
- Impulse response functions represent the response of the endogenous variables of a given system, when one (or more than one) of its endogenous variables is hit by an exogenous shock.
- The nature of the shock can be:
- Temporary
- Permanent
- Systematic
- Linear systems. The magnitude of the shock does not change the stability properties of the system.
- Nonlinear systems. In this case, the magnitude of the shock is of great inportance and it can change the stability of the system under consideration.
An example
- Consider the simplest case, an AR(1):
\[\qquad \qquad y_{t+1}= {\color{blue}a} y_{t}+\varepsilon_{t+1}, \quad \varepsilon_{t} \sim N(0,1) \tag{2}\]
- Assume that for \(t \in(1,n)\): \[y_{1}=0 \ ; \ \varepsilon_{2}=1 \ ; \ \varepsilon_{t}=0 \ , \ \forall t\neq2\]
- This implies that at \(t=2 \Rightarrow y_2 = 1\). But what happens next, if there are no more shocks?
- The IRF of \(y\) provides the answer.
- The dynamics of \(y\) will depend crucially on the value of \(\color{blue}a\). Six examples: \[\color{blue} a = \{0,0.5,0.9, 0.99, 1, 1.01\}\]
The IRFs of the AR(1) Process
\(~\)
Another example
- Consider a more sophisticated case, an AR(2):
\[y_{t+1}= {\color{blue}a} y_{t}+{\color{red}b} y_{t-1} + \varepsilon_{t+1}, \quad \varepsilon_{t} \sim N(0,1)\] * Assume that for \(t \in(1,n)\): \[y_{1}=0 \ ; \ y_2=0 \ ; \ \varepsilon_{3}=1 \ ; \ \varepsilon_{t}=0 \ , \ \forall t\neq 3\]
This implies that at
\[t=3 \ , \ \varepsilon_{3}=1 \ \Rightarrow \ y_3 = 1.\]What happens next, if there are no more shocks? The IRF of \(y\) provides the answer.
The dynamics of \(y\) will depend on the values of \(\color{blue}a\) and \(\color{red}b\). For simplicity consider: \[{\color{red}b = -0.9} \ ; \color{blue} a = \{1.85,1.895,1.9,1.9005\}\]
The IRFs of the AR(2) Process
\(~\)
More Sophisticated Examples
A similar reasoning can be applied to our rather more general model: \[X_{t+1}= A + BX_{t}+ C\varepsilon_{t+1} \tag{3}\]
.. where \(B , C\) are \(n\times n\) matrices, while \(X_{t+1}, X_{t}, A, \varepsilon_{t+1}\) are \(n\times 1\) vectors.
Consider the following VAR(3) model: \[X_{t+1}=\left[\begin{array}{c} z_{t+1} \\ w_{t+1} \\ v_{t+1} \end{array}\right]\]
In this example we take matrices \(A, B\) and \(C\) given by: $$
\[\begin{gathered} A=\left[\begin{array}{c} 0.0 \\ 0.0 \\ 0.0 \end{array}\right], \quad B=\left[\begin{array}{rrr} 0.97 & 0.10 & -0.05 \\ -0.3 & 0.8 & 0.05 \\ 0.01 & -0.04 & 0.96 \end{array}\right] , \quad C=\left[\begin{array}{lll} {\color{blue}1.0} & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 \end{array}\right] . \end{gathered}\]$$
The initial state of our system (or its initial conditions) are: \(z_{1}=0, w_{1}=0\) and \(v_{1}=0\), that is: \[X_{1}=[0,0,0]\]
The shock only hits the variable \(z_t\) \((\)notice the blue entry in matrix \(C)\), and we assume that the shock occurs in period \(t=3\).
What happens to the dynamics of the three endogenous variables? See next figure.
The IRFs of our VAR(3) Process
\(~\)
AR(1): A Sequence of Shocks
Consider the same AR(1) as in eq. (2). But now impose a sequence of 200 shocks.
\(~\)
Implications of a Linear Structure
- In the previous examples, the structure of all our models was linear.
- This has a crucial implication: The shock’s magnitude did not alter the dynamics produced by the shock itself.
- Only the structure of the model would lead to different outcomes.
- This does not usually occur if the structure of the model is non-linear. In this case, the magnitude of the shock may produce different outcomes even if the system’s structure remains the same.
- We do not have time to cover this particular point.
- But be careful: if the structure of the model is non-linear, large shocks can not be simulated … in a linearized version of the original system.
3. Important Problems
Three Major Issues
- There is no perfect filter … but the HP seems the best.
- Measuring Potential GDP (or Natural Unemployment) is difficult:
- Potential GDP is usually associated with the HP-trend in GDP … but not exclusively.
- The Natural Rate of Unemployment is largely associated with the HP-trend in unemployment.
- All macroeconomic models are non-linear:
- Be careful with IRFs that are produced by a linearized version of the model.
- Big shocks are difficult to be fully represented by linearization.
Limitations of the HP Filter
- New data leads to the rewriting of the history of the economy
- The HP filter is extremely useful but should be used with care
| |
|  |
|
Misuses of the HP Filter
- In 2012, the US economy had an unemployment rate close to 8%, one of the highest rates since WWII.
- The Fed Funds Rate was at 0%, to stimulate the economy.
- The inflation rate was much below the target level (2%) at 0.5% and showing signs of going down.
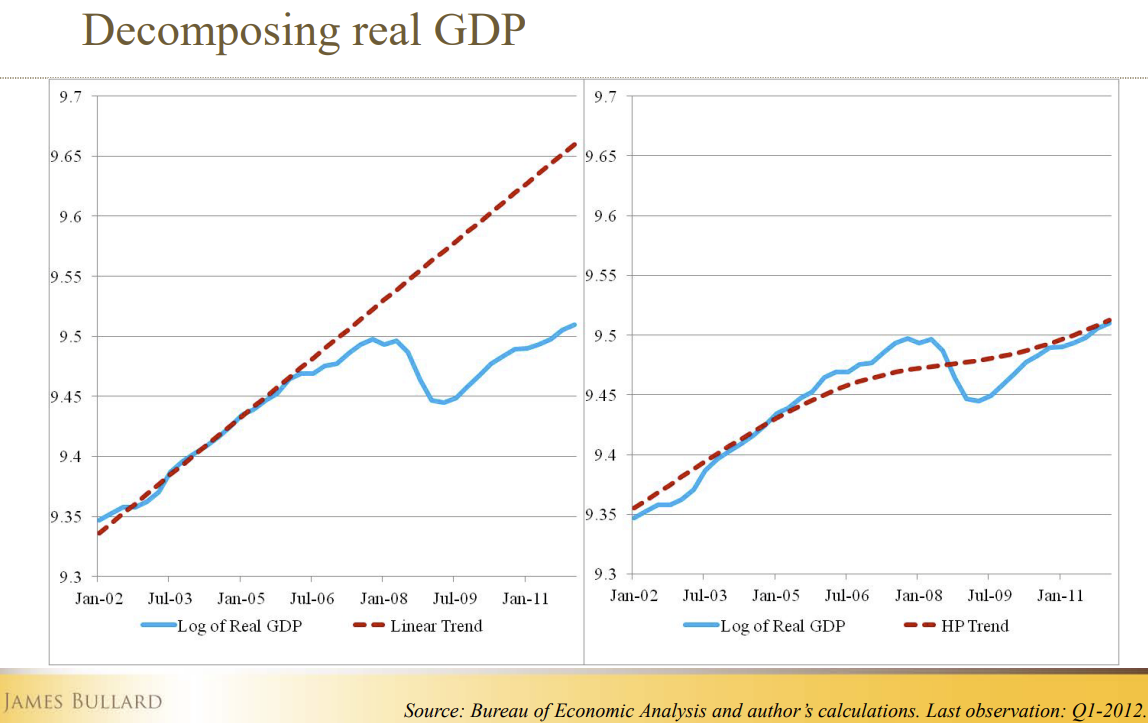
- James Bullard (the President of the FRB of St. Louis), in a famous speech in June 2012 defended that the US economy had gone back to Potential GDP.
- He defended that the Fed should produce a sharp increase in the Fed Funds Rate.
- He used the HP-filter to substantiate his proposal.
The HP filter according to James Bullard
\(~~~~~~~~\)
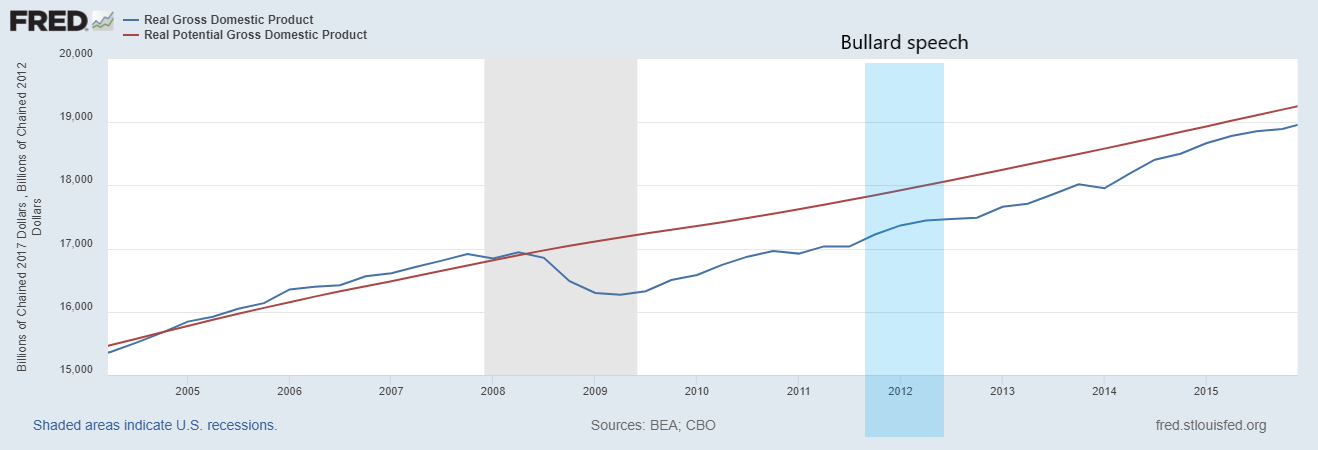
The Output-gap According to the FRB … St. Louis
The FRB of St. Louis publishes “oficial” US data for Real GDP and Potential GDP.
\(~~~~~~~~\)
The Natural Rate of Unemployment (NRU)
No, Covid-19 did not raise the NRU; no, an increase in NRU did not anticipate Covid-19!
\(~~~~~~~~\)
4. Readings
Point 1
For this point, there is no compulsory reading.
However, Dirk Krueger (2007). “Quantitative Macroeconomics: An Introduction” (Chapter 2), manuscript, Department of Economics University of Pennsylvania, is well suited for the material covered here.
This text is a small one (12 pages), easy to read, and beneficial for studying the stylized facts of business cycles, mainly to understand how the Hodrick-Prescott filter is calculated. However, notice that, as mentioned, it is not compulsory reading.
Point 2
- For this point, there is no compulsory reading. However, any modern textbook on time series will cover this subject.
- At an introductory level, see sections 11.8 and 11.9 of the textbook: Diebold, F. X. (1998). Elements of forecasting. South-Western College Pub, Cincinnati.
- At a more advanced level, see, e.g., section 2.3.2 of the textbook: Lütkepohl, H. (2007). New introduction to multiple time series analysis (2nd ed.), Springer, Berlin.
Point 3
- No textbook covers the topics/controversies mentioned in this section.
- This coursework intends to provide a framework for a better understanding of these controversies at the end of the course.
- All we have to handle is:
- A little bit of mathematics
- A little bit of computation
- A little bit of macroeconomics